|
2009-2010
Jeudi 24 Septembre :
Masahiro
Shiota (Nagoya) : o-minimal Hauptvermutung.
Résumé : Let R
be a real closed
field with an o-minimal structure which expands the semialgebraic
structure.
If two compact (=bounded and closed in Rn)
polyhedra are definably homeomorphic, they are PL homeomorphic.
Jeudi 15 Octobre :
Kartoué
Mady Demdah : Théorème de h-cobordisme semi-algébrique:
Validité sur tout corps réel clos, borne uniforme et non effectivité.
Résumé : Je presenterai la version
semi-algébrique des théorèmes de h-cobordisme et s-cobordisme valides
sur tout corps réel clos. Précisément partant d'un cobordisme
semi-algébrique, on obtient un homéomorphisme de trivialisation
semi-algébrique dont on peut borner la complexité en fonction de celle
du cobordisme. Je parlerai aussi de la non effectivité de la borne.
Jeudi 22 Octobre (reporté)
:
Frédéric
Bihan (Chambéry) : Bornes fewnomiales pour des
systèmes polynomiaux spéciaux
Résumé:
On applique nos
méthodes pour donner des bornes fewnomiales
sur le nombre de solutions de systèmes polynomiaux non génériques pour
un support donné.
Les bornes obtenues raffinent grandement celles obtenues dans le cas
générique.
(travail en commun avec F. Sottile)
du 26 au 30 Octobre
Rencontre
"Singularités réelles en analyse et géométrie".
Jeudi 26 Novembre :
Sabine
Burgdorf (Konstanz-Rennes) : Le problème des
moments : une version non commutative .
Résumé : L’étude
des polynômes positifs en des indéterminées commutatives est associée
au problème des moments. Je m’intéresse aux polynômes en des
indéterminées non commutatives qui ont une trace positive. Pour ces
polynômes on peut définir des moments de sorte qu’on a une relation
comme dans le cas commutatif entre les moments et les polynômes avec
une trace positive. Dans l’exposé j’expliquerai le problème des moments
dans cette situation et
je présenterai quelques résultats comparables à ceux de Curto et
Fialkow dans le cas commutatif.
Jeudi 21 Janvier (avec le
séminaire de géométrie analytique):
Mustafa
Korkmaz (Ankara): Actions of mapping class
groups.
Résumé:
Mapping class group of an
orientable surface is the group of isotopy classes of self
homeomorphisms of the surface. This group plays a central role in low
dimensional topology. Therefore, its algebraic properties are of
interest. In this talk, after introducing the mapping class group and
the motivation to study, I will give some known algebraic properties.
Some of these properties are obtained from its action on various
simplicial complexes.
Jeudi 28 Janvier :
Ilia
Itenberg (Strasbourg) : Sur le spectraèdre quartique dans
R3
Résumé : À trois matrices carrées
symétriques A,
B
et C de
taille 4
qui ont des coefficients réels,
on peut associer une surface spectrale dans C3
(c'est l'ensemble des points (x,
y,
z)
dans C3
tel que le déterminant de la matrice Id + xA + yB + zC est nul)
et un spectraèdre dans R3
(c'est l'ensemble des points (x,
y,
z)
dans R3
tel que la matrice Id + xA
+ yB + zC
est semi-définie positive).
En général, la surface spectrale considérée a 10 points doubles.
On s'intéresse au nombre de points doubles de
la surface spectrale qui appartiennent
à la frontière du spectraèdre,
et on montre que ce nombre n'excède pas 9.
Jeudi 4 Février :
Benoît
Bertrand (Toulouse) : Sur le nombre de composantes
connexes de la courbe parabolique.
(en commun avec Erwan Brugallé)
Résumé : La courbe parabolique d'une surface
S
est le lieu où sa courbure de
Gauss s'annule. Si S
est le graphe d'un polynôme de degré d,
l'inégalité de Harnack implique que la courbe parabolique ne peut pas
avoir plus de (2d
- 5)(d - 3)+1
composantes connexes. Quel est le nombre
maximal de composantes que peut effectivement avoir la courbe
parabolique (problème de V. Arnold 2000-1)? A. Ortiz-Rodriguez a
construit des polynômes dont la courbe parabolique a (d-1)(d-2)/2
composantes connexes. J'expliquerai comment en appliquant la méthode
de Viro à des courbes hessiennes on peut obtenir des courbes
paraboliques ayant asymptotiquement deux fois plus de composantes
connexes.
Jeudi 11 Février :
Yuriy
Savchuk (Leipzig) : Non-commutative
17th Hilbert problem
Résumé : 17th Hilbert problem asks if every
positive polynomial in n variables with
real coefficients is a sum of squares of rational functions. One can
state
a noncommutative analogue of the 17th Hilbert problem, that is, replace
the
algebra of polynomials by a noncommutative ring. I will give an
introduction to this topic and an overview over the most important
results
and methods.
Jeudi 4 Mars :
Mickaël
Matusinski (Konstanz) : Théorème de Puiseux
différentiel dans des corps de séries
généralisées de rang fini.
Résumé : Soit Kr := R((Γr)) un
corps de
séries généralisées de rang fini
r,
muni d’une dérivation de Hardy. Etant donné un ordre de dérivation n
quelconque fixé, nous
considérons des équations différentielles
(1) : F(y,y',...,y(n)) = 0
où F est
une série formelle en n
+1
variables avec des coefficients dans
Kr.
Notre objet
est de montrer comment l’ensemble des exposants d’une solution
y0
de (1) dans
Kr,
i.e. son support Supp y0,
se
déduit de manière finie de l’ensemble Supp F
des exposants des coefficients de
l’équation.
Mardi 9 Mars :
Polynômes positifs non
commutatifs
(Rencontre
dans le cadre du programme Franco-Slovène de coopération scientifique
PROTEUS)
Salle 004
| 9h-9h45 |
Igor Klep
(Ljubljana), Relaxing LMI’s noncommutatively |
| 10h15-11h |
Ronan Quarez
(Rennes 1), On positivity certificates for matrix polynomials |
| 14h-14h45 |
Markus
Schweighofer (Konstanz), Introduction to the BMV
Conjecture
|
| 15h00-15h45 |
Sabine
Burgdorf (Konstanz-Rennes 1), TBA |
| 16h15-17h00 |
Jakob
Cimpric (Ljubljana),
Noncommutative Positivstellensätze for pairs representation-vector |
Jeudi 11 Mars :
Markus
Schweighofer (Konstanz) : Pure states,
positive matrix polynomials and sums of hermitian squares (joint work
with Igor Klep)
Résumé : Let M
be an archimedean
quadratic module of real t-by-t matrix
polynomials in n
variables, and let S
be the set of all n-tuples
where
each element of M
is positive semidefinite. Our key finding is a
natural bijection between the set of pure states of M and the cartesian
product of S
with the real projective (t-1)-space.
This leads us to
conceptual proofs of positivity certificates for matrix polynomials,
including the recent seminal result of Hol and Scherer: If a symmetric
matrix polynomial is positive definite on S, then it belongs
to M. We
also discuss what happens for non-symmetric matrix polynomials or in
the absence of the archimedean assumption, and review some of the
related classical results. The methods employed are both algebraic and
functional analytic.
Jeudi 18 Mars :
Guillaume
Valette (Kraków ),
Cohomologie L∞
et homologie d'intersection
Résumé: Je donnerai un théorème de type de
Rham pour les formes
différentielles
sur les ensembles sous-analytiques.
Jeudi 1er avril :
Goulwen
Fichou : Poids dans les fonctions zeta réelles
Jeudi 27 mai :
Andrei
Gabrielov (Purdue) : Approximation of definable sets by compact
families.
Lundi
31 mai, 14 h. :
Andrei
Gabrielov (Purdue)
: Semi-monotone sets and
regular cell decomposition.
Jeudi
10 juin :
Patrick
Speisseger (McMaster, Hamilton) : O-minimalité et le 16ème
problème de Hilbert
Résumé : Soit
F
la famille de tous les champs de vecteurs polynomiaux de degrée d dans le plan. Le
16ème problème de Hilbert postule l'existence d'une borne finie sur le
nombre de cycles limites des champs appartenant à F. La conjecture de
Roussarie réduit ce problème à une version locale dans l'espace des
paramètres. Dans un travail récent avec Kaiser et Rolin, nous utilisons
l'o-minimalité pour établir la conjecture de Roussarie dans un cas très
particulier, celui d'une famille analytique ne possédant que des
singularités hyperboliques non-résonnantes. Nous espérons étendre notre
approche à un cas générique, celui d'une famille analytique ne
possédant que des singularités hyperboliques. Un ingrédient de notre
approche est la réduction aux croisements normaux dans une classe
quasi-analytique et logarithmique - exponentielle de fonctions en
plusieures variables.
Jeudi
17 juin :
Michel
Raibaut (Nice) : Une fibre de Milnor motivique
à l'infini
Résumé : Soit U une variété algébrique complexe lisse et f un morphisme non constant défini sur U. Par application du théorème de Thom-Mather,
il existe un réel R > 0 tel que f : U- f-1(D(0,R)) --> C - D(0,R)
est une fibration topologique localement triviale. La fibre de cette
fibration est appellée fibre de Milnor à l'infini. Ses groupes de
cohomologie à support compact sont munis d'une "structure de Hodge
mixte limite à l'infini". Un invariant classique associé est le
"spectre à l'infini" de f.
Mardi
22 juin, 10 h.30 :
Saugata Basu (Purdue) : A complex analogue of Toda's theorem.
Résumé : Toda's theorem in discrete
complexity theory relates the computational hardness of counting with
the polynomial time hierarchy. A real analogue of Toda's theorem in the
Blum-shub-Smale model has recently being proved. In this talk I will
describe a complex analogue of the same result. I will also sketch how
one might expect to prove the original theorem of Toda's using
topological methods.
Jeudi 24 juin :
Ludovico
Pernazza (Pavia) : Sur la régularité des racines de polynômes dépendant d'un paramètre
Résumé : En général il y a plusieurs choix
possibles de systèmes de racines pour un polynôme dont les
coefficients dépendent d'un paramètre. On peut montrer que si
toutes les racines sont réelles, la multiplicité des
racines est au plus k et les coefficients sont de classe C2k, il y a des systèmes de racines de classe C1
admettant partout une dérivée seconde. Le résultat peut
être amélioré si l'on veut trouver une bonne racine carrée
d'une fonction non négative ; il est aussi intéressant de
rapporter ces résultats au cas des polynômes admettant des
racines non réelles. 2008-2009
Jeudi
11 Septembre :
Tim
Netzer (Constance) : Positive polynomials on
large subsets of Rn.
Résumé : In Real Algebraic Geometry, the
notion of a "stable" quadratic module
has turned out to be very usefull in several contexts - for example it
allows to apply model theoretic arguments and helps settling the Moment
Problem. The core of all the previous efforts concerning stable
quadratic modules is the following:
Let K be a
subset of Rn. When
adding two real polynomials f
and g that
are nonnegative on K,
cancelling of high degree parts may result in a
polynomial f+g of much smaller
degree than the one of f
and g. But
can
there be arbitrary grave cancelling?
This question seems to be hard to decide in general. However, the
answer can only be "no" for large sets - a necessary condition for the
impossibility of grave cancelling is the absence of nontrivial bounded
polynomials. In this talk, we discuss to which extend this condition is
already sufficient.
Jeudi
18 Septembre :
Daniel
Plaumann (Constance) : Sums of squares on
reducible real curves.
Résumé : We ask whether every polynomial
function that is non-negative
on a real algebraic curve can be expressed as a sum of squares in the
coordinate ring. Scheiderer has classified all irreducible curves for
which this is the case. For reducible curves, we show how the answer
depends on the configuration of the irreducible components and give
complete necessary and sufficient conditions. We also discuss partial
results in the more general case of finitely generated preorderings and
applications to the moment problem for semialgebraic sets.
Jeudi
25 Septembre :
Michel
Coste : Diamètre géodésique d'intersection de quadriques
(travail de Moussa Seydou)
Résumé : Les
majorations connues pour le diamètre géodésiques (d'Acunto - Kurdyka)
sont exponentielles en le nombre de variables. Je présenterai le
travail de Moussa Seydou qui établit une borne polynomiale en le nombre
de variables, pour une intersection d'un nombre donné de quadriques,
dans le style du résultat obtenu par A. Barvinok pour la somme des
nombres de Betti.
Jeudi
30 Octobre
:
Mohammed
Bekkar (Oran)
: Surfaces minimales dans les espaces de Heisenberg.
Jeudi
13 Novembre
: Ilia Itenberg (Strasbourg)
: Sur
le nombre de composantes connexes
d'une intersection complète
de quadriques réelles
Résumé
:
Les résultats principaux de
l'exposé portent
sur les intersections complètes de trois quadriques réelles.
On s'intéresse au nombre maximal B02(N)
de composantes connexes qu'une intersection complète
régulière de trois quadriques réelles
dans PN
peut avoir.
On montre que le nombre B02(N)
diffère au plus de 1
du nombre maximal d'ovales de profondeur [(N-1)/2]
d'une courbe algébrique réelle plane et projective de
degré N+1.
Comme conséquence, on obtient une borne inférieure N2/4
+ O(N) et une borne supérieure
3 N2/8 + O(N) pour le nombre
B02(N). Travail
en commun avec A. Degtyarev et V. Kharlamov.
Jeudi
27 Novembre
: Markus Schweighofer :
Ensembles semi-algébriques convexes, inégalités matricielles linéaires
et sommes de carrés
Résumé : Pour
traiter les systèmes d'inégalités linéaires, on dispose des méthodes
numériques extrêmement efficaces comme l'optimisation linéaire. Mais
ces systèmes ne permettent que d'écrire des polyèdres. Les inégalités
matricielles linéaires (LMI) sont une généralisation des systèmes
d'inégalités linéaires. Tout en admettant presque autant de
possibilités algorithmiques, ils ont une expressivité très surprenante
dont témoignent des résultats récénts de Helton, Nie et Vinnikov. La
seule condition nécessaire connue en ce moment pour un ensemble d'être
défini par un LMI avec ou sans variables additionnelles est d'être
respectivement semi-algébrique convexe ou rigidement convexe. Il semble
même possible que ces conditions sont déjà suffisantes. Il y a un lien
surprenant avec le sujet très classique de l'écriture des polynômes
positifs à l'aide de sommes de carrés. Cet exposé est une introduction
au sujet avec des nouvelles contributions récemment obtenues en
collaboration avec Tim Netzer et Daniel Plaumann.
Jeudi
4 Décembre
: Jean-Philippe
Monnier (Angers)
: Diviseurs tres speciaux sur les courbes reelles.
Résumé: On étudie les systèmes linéaires
spéciaux sur une courbe
réelle dont les dimensions ne vont pas satisfaire une inégalité donnée
par Huisman. En particulier, on classifie tous ces systèmes linéaires
lorsqu ils sont non-simples.
Mercredi
17 Décembre, 14h.
: Georges Comte (Nice)
: Propriétés locales des ensembles définissables p-adiques.
Résumé : Je parlerai d'un travail en cours
en commun
avec R. Cluckers
et F. Loeser dans lequel nous étudions les propriétés métriques locales
des ensembles semi-algébriques ou sous-analytiques p-adiques. Pour ces
ensembles
on peut, comme en réel, définir la densité locale en chacun de leurs
points.
Celle-ci peut alors se calculer de différentes façons, soit par une
formule
du type Crofton locale, soit par une formule du type de celle établie
par Thie
pour les ensembles analytiques complexes, c'est-à-dire à l'aide du cône
tangent. Cette dernière formule nécessite une définition appropriée du
cône tangent en p-adique.
Jeudi
8 Janvier : Erwan Brugallé (Paris
6) : Utilisation des modifications tropicales.
Jeudi
22 Janvier
: Adam Parusinski (Angers)
: Filtration par le poids pour les variétés algébriques
réelles
Résumé : Pour toute variété
algébrique réelle nous construisons
une filtration géométrique fonctorielle sur les
chaînes semi-algébriques fermées. La suite spectrale associée
induit une filtration sur l'homologie de Borel-Moore à coefficients
dans Z/2Z, qu'on appelle filtration par les poids.
La filtration par les poids peut aussi être obtenue par la résolution
des singularités et une construction abstraite dû à Guillen et
Navarro-Aznar, une approche similaire donne dans le cas complexe la
filtration par le poids de Deligne.
Dans cet exposé nous présentons les propriétés basiques de la
suite spectrale et de la filtration par les poids,
et donnons quelques applications.
Nous discutons aussi la relation avec la théorie des formes
quadratiques.
Jeudi
5 Février
: Frédéric
Mangolte (Chambéry)
: Une généralisation au cas singulier d'un théorème de Comessatti sur
les surfaces rationnelles réelles
Séminaire
reporté pour cause de grève des enseignants-chercheurs
Résumé: Soit X une surface
géométriquement rationnelle définie sur R et M une composante
connexe de
X(R).
D'après un théorème célèbre de Comessatti, si X est
non-singulière et M
orientable, alors M
est une sphère ou un tore.
Avec F. Catanese, nous avons montré que si X admet des
singularités Du
Val et M
est l'espace total d'un orbifold orientable, alors M est
sphérique ou euclidien.
Mais le cas non-orientable réservait une surprise : en effet lorsque X
est minimale et non-singulière, M
ne peut pas être de type
hyperbolique.
Nous avons construit un exemple singulier où X est minimale et M est de
type hyperbolique.
Ces résultats ont notamment des applications à la classification des
variétés réelles de dimension 3 qui sont rationnellement connexes.
Jeudi
26
Mars: Daniel
Pecker (IMJ, Paris 6) : Nœuds de Chebyshev
Vendredi 3 Avril: Johannes
Nicaise (Lille) : Titre à préciser. Cet exposé fait suite
à un exposé de Julien Sebag au séminaire de géométrie algébrique.
Mercredi 8 avril,
14h.
: Patrick
Popescu-Pampu (Paris
7)
: Topologie des fibres de Milnor des quotients cycliques de
surfaces
Résumé: Etant donné un
germe de surface complexe a singularité isolée,
son bord est une variéte compacte de dimension 3 portant une
orientation et une structure de contact canoniques.
La theorie des déformations de la singularité fournit un
nombre fini, a difféomorphismes près, de remplissages de Stein
de ce bord de contact, les fibres de Milnor de la singularité.
C'est un probleme tres largement ouvert de décrire ces
fibres de Milnor parmi les remplissages de ce bord de contact.
Je décrirai la preuve d'une conjecture de Lisca, obtenue en
collaboration avec Nemethi, qui montre que pour les singularités
quotients cycliques (dont les bords sont des espaces lenticulaires),
les fibres de Milnor fournissent a difféomorphisme près tous les
remplissages de Stein.
.
Jeudi
23
Avril: Karim
Becher (Konstanz) :Sommes de carrés dans le corps des
fonctions d'une courbe
Résumé: Le nombre de Pythagore d'un corps K est le plus petit
entier n
tel que tout élément totalement positif de K s'exprime comme
une somme de n
carrés dans K.
Je donnerai d'abord un survol sur les bornes connues et les problèmes
ouverts liés à cet invariant de corps.
Ensuite, j'expliquerai des résultats d'un travail en commun avec David
Grimm et Jan Van Geel, qui concernent le cas d'un corps des fonctions
en une variable sur un corps valué complet k. En particulier,
on obtient que le nombre de Pythagore d'un tel corps
de fonctions est inférieur ou égal à 3 dans le cas où k = R((t)).
A la base de ces résultats est un nouveau principe local-global pour
les formes quadratiques sur de tels corps, qui a été developpé par
Harbater, Hartmann et Krashen et par Colliot-Thélène, Parimala et
Suresh.
Jeudi
14 Mai 9h.:
Ilia
Itenberg (Strasbourg) : Invariants de Welschinger et
congruences modulo 4
Résumé : Les invariants de Welschinger sont
des analogues réels
d'invariants de Gromov-Witten de genre zéro.
L'approche tropicale basée sur le théorème
de correspondance de G. Mikhalkin permet
de calculer les invariants de Welschinger
dans un certain nombre de cas.
En particulier, G. Mikhalkin a démontré des congruences modulo 4
pour les invariants de Welschinger
des surfaces toriques de Del Pezzo.
En utilisant l'approche tropicale, on établit
des congruences modulo 4
pour les invariants de Welschinger
du plan projectif éclaté en 4 ou 5 points réels
(travail en commun avec V. Kharlamov et E. Shustin)
Jeudi 14 Mai 14h.: Johannes Huisman
(Brest) : Espaces de modules de fibrés vectoriels stables
sur une courbe algébrique réelle
Résumé: Soit X une
courbe algébrique réelle
lisse et projective. D'après Mumford, l'espace des modules
Mr,d des
fibrés vectoriels stables sur
X de rang r et
de degré d est une
variété algébrique réelle quasi-projective.
Elle est projective lorsque r et d
sont premiers entre
eux. Nous déterminons quelques invariants topologiques de
l'ensemble des points réls de Mr,d
tels que les
π0, π1 et π2.
Pour ce faire on adapte des techniques de Narasimhan-Seshadri et de
Atiyah-Bott, et on étudie des représentations
unitaires du groupe fondamental équivariant de X,
et des connexions équivariantes plates à travers
la fonctionnelle de Yang-Mills.
(Travail en collaboration avec Indranil Biswas et Jacques Hurtubise.) Jeudi
4 Juin : Karim Bekka
: Rayon uniforme et conditions de régularités.
Résumé : Pour montrer qu'une famille de
germes de fonctions ou d'applications a le
même type topologique, on utilise la stratification canonique induite
par
cette famille et on étudie sa régularité, en particulier "la
propriété de rayon uniforme'' qui assure la constance du type
topologique.
Je parlerai dans cet exposé de certaines relations entre nombre de
Milnor, rayon
uniforme et conditions de Whitney.
Mercredi 10 Juin (14h) : Toshizumi Fukui (Saitama)
: Lipschitz property of blow-analytic maps
Jeudi 18 Juin (14h) :Abdelhafed Elkhadiri (Univ. Ibn Tofail, Kenitra)
: Sur un anneau noethérien de germes différentiables sur un corps réel clos
Résumé: Soit R un corps réel clos. On désigne par ER,n l'anneau des germes de fonctions
infiniment différentiables au voisinage de l'origine dans Rn. Pour tout entier naturel n,
nous construisons un sous-anneau AR,n de ER,n avec quelques propriétés naturelles.
Nous démontrons que AR,n est un anneau noethérien et que, si
R = R (le corps des réels), alors AR,n est l'anneau des germes de fonctions analytiques réelles.
Enfin nous prouvons le théorème des zéros réels et le 17e problème de Hilbert
pour l'anneau AR,n.
Année 2007-2008
Jeudi
20 Septembre
Dmitry
Novikov (Weizmann Institute of Science) : Limit
cycles appearing in polynomial perturbations of Darboux integrable
systems.
Résumé : We prove an existential
finiteness result for integrals of rational one-forms over the
level-curves of Darbouxian integrals
Jeudi
4 Octobre
Johannes
Huisman (Brest) : Surfaces rationnelles réelles
et difféomorphismes algébriques.
Mercredi
17 Octobre
Frédéric
Mangolte (Chambéry) : Modèles
algébriques réels des
variétés de dimensions 3
Résumé : En partant de
l'énoncé du théorème de
Comessatti de 1914 sur
le type topologique d'une surface rationnelle réelle, nous
chercherons
à expliquer certaines motivations des recherches
récentes (1999, 2005,
2007) sur la topologie des variétés
réelles projectives de dimension 3
Jeudi
25 Octobre
Jean-Jacques
Risler (Paris 6) : Déformations de Harnack
d'une branche plane réelle.
Résumé : Apres
une présentation des résultats de Mikhalkin sur
les
courbes (algébriques) de Harnack, on définira les
déformations "Multi-Harnack " d'une branche analytique
réelle plane singulière afin de
généraliser
pour celles-ci le résultat de Mikhalkin. On
évoquera
aussi quelques propriétés métriques de
ces
déformations : taille des ovales, concentration de la
courbure.
Le travail présenté est
réalisé en commun
avec Pedro Gonzales Peres.
Jeudi
10 Janvier
Xavier
Caruso : Extensions totalement réelles.
Application à la diagonalisation des matrices
symétriques.
Résumé :
Après avoir défini (ou rappelé la
définition de) la notion
d'extension totalement réelle d'un corps quelconque, et
après l'avoir
illustré par plusieurs exemples, j'expliquerai comment elle
intervient
de façon centrale dans un théorème de
Krakowski qui classifie les corps sur lesquels toute matrice
symétrique est diagonalisable. Je donnerai aussi quelques
indications sur la façon dont ce résultat
pourrait s'étendre à un anneau (voire un
schéma) quelconque. L'exposé apparaîtra
essentiellement comme un survol de résultats de la
deuxième moitié du 20ème
siècle.
Jeudi
17 Janvier
Ilia
Itenberg (Strasbourg) : Equivalence
logarithmique d'invariants de Welschinger
et d'invariants de Gromov-Witten.
Résumé : Les
invariants de Welschinger sont
des analogues réels d'invariants de Gromov-Witten de genre
zéro. L'approche tropicale basée sur le
théorème de correspondance de G. Mikhalkin permet
de
calculer les invariants de Welschinger dans plusieurs situations. Dans
l'exposé, on établira une équivalence
logarithmique d'invariants de Welschinger et d'invariants de
Gromov-Witten dans le cas des collections
génériques de
points réels dans un plan projectif eclaté en 4
points
réels. La démonstration est basée sur
une nouvelle
version du théorème de correspondance.
Jeudi
31 Janvier
Erwan
Brugallé (Paris)
: Décompositions en étages de courbes
tropicales
Résumé : Le but de cet
exposé est de d'appliquer la géométrie
tropicale
en géométrie énumérative
réelle et complexe. Le problème est de calculer
le nombre de courbes rationnelles projectives passant par une
configuration de sous espace linéaires fixés
(appelés contraintes). Une
technique standard en géometrie complexe est de
dégénérer la
configuration des contraintes de telle sorte que les courbes
considérées
se "cassent" en des courbes plus simples, puis d'appliquer l'invariance
du nombre de courbe par rapport à la configuration. En
utilisant une
configuration des contraintes "à la Caporaso-Harris" dans le
contexte
tropical, on observe, sans passage à la limite, la
décomposition des
courbes en morceaux simple. De plus, ces décompositions
permettent
d'obtenir des résultats sur le nombre de courbes
réelles passant par une
configuration réelle de contraintes. (travail en
collaboration avec
Grigory Mikhalkin)
Jeudi
7 Février
Giovanni
Morando (Padova)
: Site sous-analytique et solutions
tempérées des D-modules
sur une
courbe complexe
Résumé : Dans cet
exposé on rappellera la définition de
site sous-analytique et du faisceau sous-analytique des fonctions
holomorphes tempérées. En suite, on utilisera ces
objets dans
l'étude des D-modules
sur une courbe complexe. En
particulier, on étudiera la propriété
de R-constructibilité
pour le complexe des faisceaux
sous-analytiques des solutions tempérées d'un D-module sur une
courbe complexe. Ensuite, etant donnée une
équation différentielle linéaire
ordinaire, on décrira ses
invariants classiques (fournis par la décomposition formelle
et les
matrices de Stokes) à travers ses solutions
tempérées.
Jeudi
6 Mars
Vincent
Grandjean : How small is the singular set of a tame set:
sur la dimension des fibres
génériques de l'espace conormal éclaté.
Résumé :
Lé et Teissier ont montré il y a plus de vingt ans dans le monde
analytique complexe que les conditions de Whitney le long d'une strate
analytique Y d'un espace analytique equidimensionnel X etaient
equivalentes à la constance de la dimension des fibres au dessus de Y
de l'éclaté (le long de Y) de l'espace conormal C(X) de X.
Dans le monde réel une condition de ce type le long d'une petite
strate n'assure en rien que les conditions de Whitney sont
satisfaites. En fait les fibres de l'espace conormal C(W) d'un
ensemble sous-analytique W au dessus d'un point w du lieu singulier
Sing(W) sont très mal connues. On a juste une borne supérieure sur la
dimension: dim (W,w) -1.
En etudiant l'eclate de C(W) de centre w, on peut décrire un peu la
fibre conormale pour des w génériques dans Sing(W).
Ce faisant quand W \ sing(W) est équidimensionnel on récupère des
informations sur la fibre de Nash de W au-dessus des points singuliers
et on déduit une relation entre le rang local r(w) de l'application de
Gauss en un w singulier générique et la dimension de sing(W) en w,
c'est-à-dire, r(w) + dim (sing(W),w) >= dim W
-1. Ainsi
une variete lisse sous-analytique avec application de Gauss
dégénérée a un bord qui doit avoir une dimension minimale.
Jeudi
13 Mars
Raf
Cluckers (Leuven/Paris)
: b-minimalité
(un premier exposé "Intégration motivique et b-minimalité a lieu à
10h30)
Résumé : (1er exposé 10h30) Dans une
introduction élémentaire, j'expliquerai l'histoire et la signification
de l'intégration motivique. Dans une deuxième partie de l'exposé,
j'expliquerai une nouvelle notion de géométrie modérée, la
b-minimalité, et en quoi elle est prometteuse dans le domaine de
l'intégration motivique. Je supposerai très peu de prérequis.
(2nd exposé 14h) Je donne la définition plus
technique de la b-minimalité (dans l'exposé 1 je donne une définition
plus intuitive en omettant quelques détails). Je développe sa théorie
et la compare avec celle de la o-minimalité. Finalement, je reviens sur
l'intégration motivique dans les cadres b-minimaux, surtout orientée
vers une interpolation des intégrales générales p-adiques et
Fp((t))-adiques. Ceci est la première version générale de l'intégration
motivique qui fonctionne aussi en caractéristique mixte pour des petits
p et pour une ramification arbitraire.
Jeudi
27 Mars
David
Burguet (Ecole Polytechnique)
: Lemme algébrique de Yomdin-Gromov et applications
dynamiques
Résumé : La théorie de Yomdin permet de
comprendre de nombreux aspects dynamiques des applications de classe Cr.
Cette theorie s'appuie sur un lemme de reparamétrisation
d'ensembles semi-algébriques (dont la forme est due a Gromov) qui
affirme que "la complexité différentielle d'un ensemble algébrique est
bornée par sa complexité algébrique". Nous présenterons les grandes
lignes de la preuve de ce lemme algébrique et nous en déduirons suivant
Gromov, Yomdin et Buzzi certaines propriétés dynamiques des applications
Cr.
Jeudi
10 Avril
Vladimir
Kostov (Nice)
: Sur la composition de Schur-Szegö de polynômes à une variable
Résumé : La composition de Schur-Szegö (CSS)
de deux
polynômes de degré
n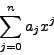 et
et 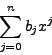 à une
variable
est définie par
la formule à une
variable
est définie par
la formule 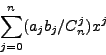 . Chaque polynôme P de
degré n
ayant une de ses racines en -1 se présente
de façon unique comme la CSS de n-1 polynômes de la
forme (x+1)n-1(x+ai), i=1,...,n-1. Si P est réel
et k, l
designent
les nombres de couples conjugués respectivement parmi les racines
de P
et
parmi les nombres ai,
alors tous les couples (k,l) sont
réalisables, . Chaque polynôme P de
degré n
ayant une de ses racines en -1 se présente
de façon unique comme la CSS de n-1 polynômes de la
forme (x+1)n-1(x+ai), i=1,...,n-1. Si P est réel
et k, l
designent
les nombres de couples conjugués respectivement parmi les racines
de P
et
parmi les nombres ai,
alors tous les couples (k,l) sont
réalisables, ![0\leq k,l\leq [(n-1)/2]](kostov/img14.png) .
Les limites (pour .
Les limites (pour 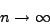 )
des
vecteurs
propres de l'application "coefficients de P" )
des
vecteurs
propres de l'application "coefficients de P" 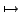 "valeurs des
polynômes
symétriques élémentaires des nombres ai"
sont définies par les
polynômes de
Narayana "valeurs des
polynômes
symétriques élémentaires des nombres ai"
sont définies par les
polynômes de
Narayana 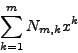 où où 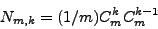 sont les
nombres de Narayana dont on rappellera l'importance combinatoire.
sont les
nombres de Narayana dont on rappellera l'importance combinatoire.
Jeudi
17 Avril
Adam
Parusiński (Angers)
: Filtration sur l'homologie des variétés algébriques réelles
Résumé : Soit X
une variété algébrique réelle. En utilisant la construction abstraite
due à Guillen et Navarro-Aznar on définit une suite spectrale E**,*
qui tend vers l'homologie (de Borel-Moore) de X à coefficients
dans Z/2Z.
Dans le cas complexe une construction analogue pour l'homologie à
coefficients
dans Q
définit la filtration par le poids de Deligne. Dans cet exposé on
définit géométriquement une filtration fonctorielle ApC*(X) sur les
chaînes semi-algébriques. Le complexe filtré ApC*(X)
représente le foncteur de Guillen et Navarro-Aznar (qui n'est défini
que dans une catégorie localisée des complexes filtrés) et par
conséquent donne
la suite spéctrale. La filtration
ApC*(X)
mesure, par
définition, la "distance"
d'une chaîne aux chaînes symétriques par arcs. Par exemple, les
homologies "pures"
coïncident avec celles représentés par les chaînes
arc-symétriques.
Jeudi
22 Mai
Dmitri
Grigoriev
: Stratifications de Thom-Whitney a-régulières universelles et
théorème de type Sard
pour des variétés singulieres.
Résumé : On dit qu'une stratification est
universelle si tous ses strates apparaissent
dans n'importe quelle stratification. On démontre qu'une stratification
de
Thom-Whitney a-régulière universelle d'une application polynomiale
existe si et
seulement si le sous-faisceau d'espaces vectoriels du faisceau
cotangent
associé à l'application est lagrangien. La démonstration utilise
une version d'un théorème de type Sard pour des variétés singulières.
Par
ailleurs, un exemple d'application est donné qui n'admet aucune
stratification universelle.
Les résultats sont communs avec P. Milman.
Vendredi
27 Juin
Toshizumi
Fukui (Saitama) : Isolated singularities of
degree n
binary differential equations.
Résumé : We study isolated singularities of
binary differential
equations of degree n
which are totally real. This means that at any regular point, the
associated algebraic
equation of degree n
has exactly n
different real roots (this
generalizes the so called
positive quadratic differential forms when n = 2). We
introduce the
concept of index
for isolated singularities and generalize Poincaré-Hopf theorem and
Bendixon formula.
Moreover, we give a classification of phase portraits of the n-web
around a generic singular
point. We show that there are only three types, which generalize the
Darbouxian classification
of umbilics. We also mention polygonal property of the subject.
This is a joint work with Juan J Nuno Ballesteros.
Année
2006-2007

Jeudi 28 Septembre
Soutenance
de la
thèse de Valéry
Mahé : Calculs dans les jacobiennes de courbes
algébriques, applications en géométrie
algébrique réelle.
Jeudi
19 Octobre
Daniel Panazzolo (Sao Paulo - Rennes) : Cycles limites pour
les
équations de Liénard : comptage de solutions de
l'équation
(...(xr1
+ a1)r2 +
...)rn
+ an=
x
.
Résumé
: Nous allons discuter le
problème de comptage
des
cycles limites pour l'équation de Liénard
classique x'
= y - P(x)
, y'
= -x ,
où P(x)
est un polynôme en x.
Une compactificaztion convenable de l'espace de tous les
systèmes de Liénard nous amène
à
considérer l'équation du titre
Jeudi
26 Octobre
Nicolas
Puignau
(Lyon) : Invariant de Welschinger et orientation relative
Résumé : Nous
aborderons les
récents
développements en géométrie
énumérative réelle.
Combien de courbes algébriques de genre 0 passent par une
collection quelconque de points dans le plan P2
?
Une approche actuelle consiste à construire des espaces de
modules spécifiques et répondre à
cette question
par un calcul (co)homologique suivant Kontsevich (en complexe) puis
Welschinger (en réel).
Dans le cadre réel il est nécessaire de prendre
en compte
l'orientation de ces espaces et c'est ce point qui sera
traité
dans la détermination de certaines classes
caractéristiques.
Jeudi
9 Novembre
Mounir
Nisse
(Jussieu) : L'aire des amibes des courbes dans (C*)2
Résumé : A toute courbe
algébrique 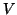 dans
dans 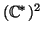 est associé
son amibe
est associé
son amibe 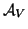 .
On
sait que le squelette .
On
sait que le squelette 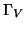 de de 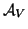 est
une courbe tropicale duale d'une subdivision
est
une courbe tropicale duale d'une subdivision 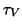 du polygone
de Newton du polygone
de Newton 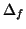 du
polynome
du
polynome 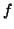 définissant
la courbe
définissant
la courbe 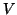 et que l'aire de
et que l'aire de 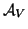 est finie. Le sujet de
l'exposé est de montrer que l'aire de l'amibe est finie. Le sujet de
l'exposé est de montrer que l'aire de l'amibe 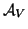 est
bornée par
est
bornée par 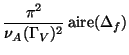 ,
où ,
où 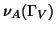 est une constante qui
ne dépend que
du
support
est une constante qui
ne dépend que
du
support 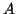 de
de 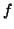 et de la
courbe
tropicale et de la
courbe
tropicale 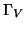 .
On montre aussi que cette
borne
est atteinte si et seulement si l'application logarithmique est au plus .
On montre aussi que cette
borne
est atteinte si et seulement si l'application logarithmique est au plus
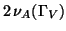 -to- -to-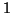 et le polynôme définissant cette courbe est
réel à une constante multiplicative
prés.
et le polynôme définissant cette courbe est
réel à une constante multiplicative
prés.
Jeudi
16 Novembre
Ilia
Itenberg
(Strasbourg) : Invariants de Welschinger des surfaces toriques de Del
Pezzo munies de structures réelles non standards
Résumé : Les
invariants de
Welschinger sont des
analogues réels
d'invariants de Gromov-Witten de genre zéro.
L'approche tropicale basée sur le
théorème
de correspondance de G. Mikhalkin permet
de calculer les invariants de Welschinger
dans plusieurs situations, et en particulier,
dans le cas des surfaces toriques de Del Pezzo
munies de leurs structures réelles standards
(c'est-à-dire, naturellement compatibles avec la structure
torique).
Dans l'exposé, on parlera d'une formule tropicale
pour les invariants de Welschinger
de surfaces toriques de Del Pezzo
munies de structures réelles non standards.
Cette formule produit des nouveaux résultats concernant
le dénombrement de courbes rationnelles réelles
sur les
surfaces
en question. (Travail en commun avec V.
Kharlamov et E. Shustin.)
Jeudi 7 Décembre
Vincent
Florens
(Genève) : Polynômes d'Alexander de courbes
algebriques
planes
Résumé : On considere
la notion de
polynôme
d'Alexander d'une courbe algébrique plane, tordu par une
représentation linéaire. On montre qu'il divise
le
produit des polynômes des entrelacs associés aux
singularités de la courbe et que
le quotient est donné par une certaine forme d'intersection.
Ce
resultat étend un théorème de
Libgober, et en
donne une interpretation géometrique.
On montre, à travers des exemples, que ces invariants
détectent certaines paires de Zariski dont les
polynômes
d'Alexander classiques coincident. Ils sont aussi sensibles aux
dégénérations nodales.
Jeudi
14 Décembre
Adam
Parusinski
(Angers) : L'equivalence blow-analytique des germes de
fonctions
analytiques
de 2 variables reelles.
Résumé : D'apres Kuo deux germes f,g : Rn
-> R
sont blow-analytiquement
équivalents (b-a équivalents) si ils deviennent
analytiquement équivalents apres des modifications
réelles des espaces sources.
Dans ce travail en collaboration avec Satoshi Koike on
considère
que
le cas n =
2. On montre que 2
tels germes sont b-a équivalents si
et seulement si leurs résolutions minimales sont isomorphes.
Ainsi
on obtient une classification complète en termes des graphes
de
résolutions ou bien des modèles d'arbre. Ensuite
on
montre que 2 germes C1-équivalents
sont b-a équivalents. On donne un exemple de 2 germes
équivalents par
un homéomorphisme bi-lipschitzien qui
ne sont pas b-a équivalents.
Jeudi 21
Décembre
David
Trotman
(Marseille) : Equisingularité de sections, condition (tr),
et la clôture intégrale des modules
Résumé: On utilise la
théorie de la
clôture intégrale des modules pour
étudier les
sections de variétés analytiques
réelles ou
complexes. Les conditions d'équisingularité
utilisées sont les conditions (tr)
introduites par
Thom et étudiées par moi-même. Je
détaillerai les raffinements récents
développés avec T.-C. Kuo et L. Wilson et les
conséquences pour la théorie de suffisance des
jets
d'applications réelles. Des nouveaux résultats,
obtenus
avec T. Gaffney et L. Wilson, incluent une nouvelle preuve simple du
théorème (de Kuo-Trotman-Wilson)
décrivant le
comportement des conditions (tr) sous une
modification de
Grassmann, et une caractérisation des conditions (tr)
utilisant la multiplicité d'un sous-module du module
Jacobien de
la singularité. Ceci donne des critères
numériques
pour l'équisingularité de Verdier.
Jeudi 25 Janvier
Frédéric
Bihan (Chambéry) : Nouvelles bornes
fewnomiales.
Résumé: La
règle de
Descartes implique qu'un polynôme réel en une
variable avec m+1
monomes distincts possède au plus 2m
racines réelles. En particulier, si le degré d'un
tel
polynôme est grand par rapport au nombre de
monômes, peu de
racines complexes sont en fait réelles. En 1980 Khovansky a
montré qu'un tel phénomène
n'était pas
propre aux polynômes en une variable. Il a en particulier
proposé une borne sur le nombre de solutions
réelles d'un
système de n
équations polynomiales en n
variables qui ne dépend que du nombre total de
monômes
distincts. Néanmoins, cette borne parait
extrêmement
grande. Dans cette exposé, on présentera de
nouvelles
bornes fewnomiales obtenues très récemment avec
Frank
Sottile. Ces bornes améliorent considérablement
celles de
Khovansky et sont asymptotiquement optimales en un certain sens.
Jeudi 15 Février
Didier
D'Acunto
(Genève) : Structure géométrique des
talwegs (ou extrémales de gradient)
Résumé : On montre que
les
ensembles
extrémaux du gradient d'une fonction
générique
lisse sont lisses en dehors des points critiques de la fonction. Aux
points critiques, les branches lisses des ensembles
extrémaux
sont tangentes aux espaces propres du hessien. De plus, la fonction est
de Morse sur son ensemble extrémal. S'il reste du temps, on
montrera également que le talweg est transverse a presque
tous
les niveaux de la fonction. Ce dernier résultat permet de
conclure sur la finitude de la longueur des trajectoires de gradient
d'une fonction lisse générique.
Vendredi 16 Février,
10h.30 (en commun avec le Séminaire de Calcul
Formel)
Saugata
Basu (Georgia Tech.) : Combinatorial Complexity in
O-minimal Geometry
Abstract: In this talk I will state some
tight
bounds on the combinatorial and
topological complexity of sets defined in terms of n definable sets
belonging to some fixed definable family of sets in an o-minimal
structure.
This generalizes the combinatorial parts of similar bounds known in the
case of semi-algebraic and semi-Pfaffian sets, and as a result
increases
the applicability of results on combinatorial and topological
complexity of
arrangements studied in discrete and computational geometry. As a
sample
application, we extend a Ramsey-type theorem due to Alon et al.,
originally
proved for semi-algebraic sets of fixed description complexity
to this more general setting.
Jeudi 1er Mars
Erwan
Brugallé (Paris 6) : Surfaces
algébriques réelles avec beaucoup de points
doubles isolés.
Résumé : Combien de
points doubles
(singularités A1)
peut avoir une surface algébrique complexe de
degré d?
D'après Miyaoka, ce nombre est asymptotiquement
borné par 4/9 * d3,
et Chmutov construisit des surfaces de degré d avec 5/12 * d3
points doubles. Pour une surface algébrique
réelle, on
peut donner une meilleure borne sur le nombre de points doubles
isolés : 5/12 * d3.
Savoir si ces deux bornes supérieures (complexes et
réelles) sont optimales est toujours un problème
ouvert.
Le but de cet exposé est d'expliquer la méthode
de
construction de Chmutov, et d'expliquer comment l'adapter pour
construire des surfaces algébriques réelles avec
1/4 * d3
points doubles isolés. J'expliquerai aussi pourquoi cette
méthode ne peut donner de meilleur résultat.
Ce travail est en commun avec Oliver Labs.
Jeudi 8 Mars
Goulwen
Fichou : Classification des singularités
simples au sens de l'équivalence de Nash
après éclatements.
Résume: L'équivalence
de Nash
après
éclatements est un analogue semi-algébrique
et analytique de l'équivalence analytique après
éclatements de T.C. Kuo.
On sait que le corang et l'indice d'un germe de fonctions Nash sont
invariants au sens de cette équivalence. On montre ici que
des germes
simples sont équivalents si et seulement s'ils le sont au
sens de
l'équivalence analytique.
Jeudi 22 Mars
Markus
Schweighofer (Konstanz) : Polynômes positifs en
variables non commutatives et problème de plongement d'Alain
Connes.
Jeudi 29 Mars
Guillaume
Rond (Toulouse) : Régularité des
morphismes d'algèbres locales.
Résumé : Je vais
parler de
résultats de régularité des morphismes
d'algèbres
locales, en particulier d'algèbres analytiques et formelles
sur C (dus
a
Gabrielov, Izumi et Tougeron entre autres). Nous allons montrer comment
un
résultat de Eakin et Harris sur la monomialisation de tels
morphismes permet
d'aborder ces problèmes et de
généraliser certains de ces résultats
à des
algèbres locales sur des corps autres que le corps des
nombres complexes.
Jeudi
5 Avril
Benoît
Bertrand (Genève) : Nombres
caractéristiques de Zeuthen réels pour deux
droites.
Résumé : Le nombre de
courbes
algébriques complexes nonsingulières de
degré d
passant par d(d+3)/2 - t points et
tangentes à t
droites est (2(d-1))t (si
la configuration est générique et t
< 2d
-1). F. Ronga a
montré que pour
une droite (t=1)
le probleme réel correspondant était maximal: il
existe une configuration générique de points et
d'une droite réels tel
que 2(d-1)
courbes réelles de degré d
passent par les
points et soient
tangentes à la droite. En utilisant la
géométrie tropicale on montre
la maximalité de ce problème
énumératif réel pour deux droites (t
= 2).
Jeudi
19 Avril
Guillaume
Valette (Toronto) : Sur le type métrique des
ensembles semi-algébriques.
Résumé: Etant
donné un
ensemble
semi-algébrique, il est possible de construire une
triangulation renfermant la totalité de son type
métrique. Ceci implique notamment un version bi-Lipschitz du
théorème de Hardt. Je donnerai aussi d'autres
conséquences de l'existence de ces triangulations pour
l'étude métrique des singularités en
géométrie semi-algébrique et
o-minimale.
Jeudi
26 Avril
Masahiro
Shiota (Nagoya - Rennes) : G-manifolds and
triangulations.
Résumé: Let G be a compact Lie
group.and M
an analytic G-manifold.
Then the orbit space M/G is Hausdorff. Let
p
: M
-> M/G denote the
canonical map. Then
Theorem (with Murayama): There exists polyhedra P and Q, a subanalytic
homeomorphism u : M -> P and a
homeomorphism v
: M/G -> Q s.t. v
p
u
-1 : P -> Q is PL.
This is known in the case of finite G.
Mercredi
2 Mai
Vincent
Grandjean (Oldenburg) : Valeurs critiques
asymptotiques et
courbure totale.
Résumé: Etant
donnée une
fonction définissable dans une structure o-minimale
fixée a priori et suffisamment différentiable, je
vais essayer de montrer quelles sont les relations entre l'existence de
valeurs critiques asymptotiques
et la continuite des fonctions coubure totale et coubure totale absolue
au voisinage de cette valeur critique asymptotique. Dans des cas
simples,
je donnerai un critère suffisant
d'équisingularité (à l'infini), au
voisinage d'une valeur régulière,
exprimé
par des conditions sur ces fonctions courbures totales.
Si j'ai encore un peu de temps, je donnerai des conditions
nécessaires et suffisantes
d'équisingularité à l'infini pour les
fonctions à bouts coniques definies dans l'espace, qui sont
similaires aux résultats plans de Tibar-Zaharia et Coste-de
la Puente.
Mercredi
16 Mai, 10h30
Masahiro
Shiota (Nagoya - Rennes) : Equivalence relations of maps.
Résumé : An
equivalence
relation on the family of 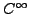 map germs is maturally defined by
local
map germs is maturally defined by
local 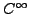 diffeomorphisms of the domain of definition and
of the
target space. There are two kind of equivalence relations of analytic
map germs - by local
diffeomorphisms of the domain of definition and
of the
target space. There are two kind of equivalence relations of analytic
map germs - by local 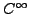 diffeomorphisms or by local
analytic diffeomorphisms. First theorem says that they are different.
In case of Nash map germs there are 3 equivalence relations - by
local
diffeomorphisms or by local
analytic diffeomorphisms. First theorem says that they are different.
In case of Nash map germs there are 3 equivalence relations - by
local 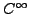 ,
analytic or Nash diffeomorphisms. Second theorem: they are the
same. Third theorem treats the global map case. ,
analytic or Nash diffeomorphisms. Second theorem: they are the
same. Third theorem treats the global map case.
Jeudi
24 Mai
Ilia
Itenberg (Strasbourg) : Sur la
réalité totale des fonctions
méromorphes
(travail en commun avec A. Degtyarev, T. Ekedahl, B.
Shapiro et M. Shapiro).
Résumé: On montre que
si tous les
points critiques d'une fonction
méromorphe de degré au plus quatre sur une courbe
algébrique
réelle de genre arbitraire sont réels,
alors cette fonction est essentiellement réelle.
Jeudi
31 Mai
Georges
Comte (Nice) : Discriminants et invariants de courbure en
géométrie réelle.
Résumé : Soit X un ensemble
sous-analytique compact de Rn,
muni d'une stratification (Xj).
On donne une condition
géométrique (G)
sur la famille
(le long d'une strate Xj)
des
discriminants des projections générales
de X
sur des plans vectoriels, qui assure la continuité
d'invariants locaux de courbure attachés aux
germes Xy,
y
dans Xj.
On montre
que si la stratification (Xj)
est (b*)
ou (w)-régulière,
la condition (G)
est réalisée. Il s'agit de la version
réelle du théorème de
Teissier selon lequel la condition de Whitney implique la
constance des multiplicités polaires en analytique
complexe. contrairement au cas complexe, on ne peut
en espérer une réciproque en
réel.
Jeudi
7 Juin
Francesca
Acquistapace et Fabrizio
Broglia (Pise) : Un panorama de la
géométrie semianalytique globale.
Résumé: Il y a
toujours deux points
de vue en géométrie analytique: local et global.
La dichotomie devient plus importante dans le cas
réel, où déjà Cartan
(années 50) remarqua les mauvaises proprietés des
espaces analytiques reels definis de façon analogue aux
espaces complexes.
Ceci l'amena à considérer la
sous-catégorie des sous-ensembles analytiques
definis par des équations globales, les C-espaces. Pour les
C-espaces on
garde beaucoup des proprietés des espaces complexes,
notamment la
decomposition en composantes irréductibles et la
possibilité d'utiliser la
théorie des faisceaux cohérents.
Le point de vue local, autrement dit le cas des germes, est
basé comme tout
le monde sait sur le théoreme de préparation de
Weierstrass. L'anneau
sous-jacent est l'anneau des séries convergentes, le
voisinage du point n'est
pas fixé.
Par contre dans le point de vue global, l'ouvert est fixé et
l'anneau est
l'anneau O(U) des fonctions
analytiques réelles sur
U.
Les problèmes qui on va considérer sont de deux
sortes:
- Propriétés
de l'anneau:
- caractérisations
des fonctions non négatives (Hilbert 17)
- Nullstellensatz,
Positivstellensatz ...
- Propriétés
des ensembles définissables par l'anneau:
- composantes
connexes des ensembles semianalytiques globaux
- fermeture
Dans
l'exposé on essaiera de donner un panorama des
résultats connus sur chacun de ces sujets pour avoir une
idée sur l'état de l'art dans ce domaine.
Jeudi
14 Juin
Alexandre
Sine (Angers) : Maximalité des
variétés toriques en dimension 4.
Résumé: Le but de cet
exposé sera de
montrer qu'une variété torique
de dimension 4
est maximale, c'est-à-dire que la somme des nombres de Betti
de
l'ensemble de ses points réels est égale
à celle
de l'ensemble de ses points complexes,
en se basant sur la méthode utilisée dans
l'article "Is
every toric
variety an M-variety?" (Clint Mc Crory, Frederic Bihan, Matthias Franz,
Joost Van Hamel 2006).
Jeudi
5 Juillet
Masahiro
Shiota (Nagoya/Rennes) : Differential topology over real
closed field
Résumé: I want to
develop differential topology over any real closed field R. It is natural to
asume an o-minimal structure on R
for the definition of a derivative of a function. Then many known
results on differential topology hold over R by
the following theorems.
Theorem.
A definable C1
manifold M
in Rn
is definably C1
diffeomorphic to a Nash manifold M'
in Rn
defined by polynomials with coefficients in Q.
Let M1,
M2
be definable C1
manifolds. Set Homd(M1,
M2)
= definable homotopy classes from M1
to M2,
and MR = the
Nash manifold defined in Rn by
the same polynomials as M'.
Theorem
There is a natural one-to-one map Homd(M1,M2)
-> Hom(M1R , M2R)
(usual homotopy classes). If M1
and M2
are definably C1
diffeomorphic, M1
R
and M2
R
are Nash diffeomorphic.
Année
2005-2006

Trimestre de
Géométrie Réelle du Centre Emile Borel (du 12
septembre au 16
Décembre 2005) : voir
le programme scientifique.
Jeudi
9 Février
Krzysztof
Grelowski : On
some extension of Hardy
fields by elements without
C-infinity representatives.
Jeudi 16
Février
Daniel Plaumann : Bounded
polynomials
and the
moment problem.
Jeudi 23
Février
Masahiro Shiota (Nagoya)
:
Definable
analytic functions.
Jeudi 16
Mars: soutenance de
l'habilitation de J-P. Monnier à Angers
Jeudi 23 Mars
Ilia Itenberg (Strasbourg)
:
Combinatoire des
courbes trigonales réelles.
Jeudi 30 Mars
Goulwen
Fichou : Nombres de Betti virtuels
equivariants.
Jeudi 6
Avril: pas de
séance (rencontre
"Sources of Real Algebraic Geometry" à Cortona)
Jeudi 13 Avril
Jean-Philippe Monnier (Angers)
: Points fixes des
automorphismes de
courbes réelles.
Jeudi 20
Avril
Nicolas Dutertre (Marseille)
: Voisinages semi-algébriques
d'ensembles semi-algébriques fermés.
Jeudi
1er Juin
Krzysztof Kurdyka (Chambéry) : Vers les structures
d-minimales: un ensemble de Cantor de dimension entropique
(exponentiellement) nulle (Travail en commun avec P. Speissegger).
Résumé
Mercredi 7 Juin, 15h30
(séance supplémentaire, salle 016)
Moussa Seydou : Diamètre géodésique des
ensembles semi-algébriques.
Jeudi 8 Juin
Alexandre Rambaud (Paris 7) :
Quasi-analyticité,
o-minimalité
et élimination des quantificateurs
Jeudi 15 Juin
Colloque
"Geometry and topology of real algebraic varieties" à Angers
Jeudi
22 Juin
Grigory Mikhalkin (Toronto - IHES) : Spatial
tropical curves
Jeudi 29 Juin
Johan Huisman (Brest) : Courbes hyperelliptiques anisotropes
et
configurations de droites
Année
2004-2005

Jeudi 9
Septembre 2004:
Masahiro Shiota (Nagoya):
Construction
of a
family of topological types of manifolds, with cardinality of the
continuum, by linear methods.
Jeudi 23
Septembre 2004:
Masahiro Shiota (Nagoya):
Whitney
triangulations.
Jeudi 7
Octobre 2004:
Mark Spivakovski
(Toulouse) : Sur la conjecture de Pierce-Birkhoff.
Jeudi 14
Octobre 2004:
James
Madden
(Baton Rouge) : The Pierce-Birkhoff conjecture and Local Real Geometry.
Jeudi 4
Novembre 2004:
Ilia
Itenberg (Strasbourg):
Variétés hyperkähleriennes réelles.
Jeudi 25
Novembre 2004:
Guillaume
Valette (Cracovie): Une version
bilipschitz du théorème de trivialisation de Hardt
Jeudi 2
Décembre 2004:
Jean-Yves
Welschinger (ENS Lyon): Invariants
relatifs des variétés symplectiques réelles de
dimension quatre.
Jeudi 6
Janvier 2005:
Serge Randriambololona
(Chambéry):
Structures o-minimales et corps de Hardy: quelques exemples.
Jeudi 13
Janvier 2005:
Mathilde
Lahaye-Hitier (Brest): Fonctions
rationnelles réel-étales.
Jeudi 27
Janvier2005:
Didier
D'Acunto (Pise/Chambéry):
Inégalité du gradient de Lojasiewicz effective.
Jeudi 3
Février2005:
Goulwen
Fichou: Le corang est un invariant de
l'équivalence de Nash après éclatement.
Jeudi 17
Février2005:
Alexei
Grigoriev (MPI Bonn): Effective
estimates on the number of zeros of Abelian integrals.
Jeudi 10
Mars 2005:
Ilia
Itenberg (Strasbourg) - sous
réserve.
Jeudi 31
Mars 2005:
Claude Viterbo
(Polytechnique) : Bornes
explicites sur des nombres
caractéristiques de variétés algébriques
réelles.
Jeudi 7
Avril 2005:
Joost
van Hamel (Leuven) : Borel-Haefliger
revisité
Mercredi 4
Mai 2005:
Thèse
de Solen Corvez : Etude de systèmes
polynomiaux : contributions à la classification d'une famille de
manipulateurs et au calcul des intersections de courbes A-splines
Jeudi 2 Juin
2005:
Johan
Huisman (Brest) : Des
uniréglées et des lenticulaires (une conjecture de J.
Kollar).
Année
2003-2004

Jeudi
18 septembre 2003:
Jesús M. RUIZ (Madrid) :
``Sums
of squares of analytic functions on curves and surfaces''.
Jeudi
2 Octobre 2003:
Louis
Mahé :
``Quelques résultats de descente pour le rang des courbes
elliptiques, et polynômes à la Motzkin".
Jeudi
9 Octobre 2003:
Ilia
Itenberg
(Strasbourg) : ``Courbes réelles rationelles sur les
surfaces de Del Pezzo toriques".
Jeudi
6 Novembre 2003:
Luis
Felipe
Tabera
: ``First steps in tropical algebraic geometry", d'après B.
Sturmfels et al.
Jeudi
13 Novembre 2003:
David Trotman (Marseille) :
"Stratifications
lipschitziennes de Mostowski, ailes génériques et
suffisance de jets".
Jeudi
20 Novembre 2003:
Johan Huisman (Brest) :
"Méthodes
analytiques en géométrie algébrique réelle".
Jeudi
27 Novembre 2003:
Erwan Brugallé : "Courbes
projectives
séparantes symétriques de degré 7: classifications
algébrique et pseudo-holomorphe".
Jeudi
4 Décembre 2003:
Karim
Bekka
:
"Sur l'algèbre des fonctions controlées".
Jeudi
8 Janvier 2004:
Didier D'Acunto (Chambéry /
Complutense
Madrid) : "Diamètre géodésique d'une composante
connexe compacte d un ensemble algebrique réel".
Jeudi
22 Janvier 2004:
Michel Coste
: "Triangulation des morphismes définissables".
Jeudi 5
Février 2004:
Goulwen
Fichou (Angers) : "Equivalence de Nash
après éclatement (questions de modules, invariants,
classification)".
Jeudi 12
Février 2004:
Luis Felipe Tabera:
"Constructions
géométriques tropicales".
Jeudi 26
Février 2004:
Ludovic
Rifford (Lyon I) : "Un
théorème de Sard pour certaines fonctions lipschitziennes"
Jeudi 4 Mars
2004:
Andreas
Bernig (Freiburg) : "Espaces tangents
des ensembles sous-analytiques".
Jeudi 11
Mars 2004:
Louis
Mahé : "Sur la conjecture de
Pierce-Birkhoff en 3 variables".
Jeudi 18
Mars 2004:
Frédéric
Bihan (Lausanne) :
"Méthode de Viro pour les intersections complètes".
Jeudi 25
Mars 2004:
Ilia
Itenberg (Strasbourg) :
"Dénombrement asymptotique de courbes rationnelles
réelles''.
Jeudi 22
Avril 2004:
Lucia
Lopez de Medrano (Jussieu):
"T-construction et points critiques des surfaces"
Jeudi 29
Avril 2004:
Patrick
Speisseger (McMaster University,
Hamilton) : "D-minimalité et une trichotomie pour les champs de
vecteurs analytiques dans le plan réel."
Résumé: Soit F un champ de
vecteurs analytique dans le plan réel, et soit T le germe
à l'origine d'une trajectoire. Supposons que l'origine est une
singularité élémentaire de F. Alors il n'y a que
trois possibilités: soit l'expansion (R,T) du corps réel
R par (l'image de)T est o-minimale, soit elle est d-minimale, soit elle
définit l'ensemble Z des entiers. Je définis la notion de
d-minimalité, et je discute son possible intérêt
comme notion au-delà de l'o-minimalité. Si le temps
permet, je mentionne aussi d'autres extensions de l'o-minimalité
avec un intérêt possible dans l'étude des champs de
vecteurs.
Jeudi 6 Mai 2004:
Jean-Philippe
Monnier (Angers) : "Theoreme de
Clifford pour les courbes algebriques reelles."
Jeudi 13 Mai
2004:
Aleksandra
Nowel (Angers/Gdansk) :
"Topological invariants of analytic sets associated with noetherian
families."
Jeudi 27
Mai 2004:
Clint
McCrory (Athens, Georgia) : "Compact
real toric varieties are M-varieties."
Abstract:
Let X be a complete
toric variety, let X(R) be its
real points, and let X(C) be its complex points. We prove that the sum
of the Z/2 Betti numbers of X(R) equals the sum of the Z/2 Betti
numbers of X(C). This is well-known for smooth complete toric
varieties. Our proof extends this result to singular toric varieties.
This is joint work with Frederic Bihan and Joost van Hamel.
Jeudi 17
Juin 2004:
Jean-Marie
Lion:
Le théorème du complémentaire pour les
sous-pfaffiens.
Mahaman Bazanfaré (Niamey):
Théorème des sphères pour les
variétés à courbure positive.
Année
2002-2003

Jeudi 12
septembre 2002:
Jesús M. RUIZ (Madrid) : ``What we know and we guess about
the Pythagoras numbers of rings''.
Jeudi 19 septembre 2002:
Masahiro SHIOTA (Nagoya): ``Triangulations of semialgebraic
maps''.
Jeudi 10
octobre 2002:
Johannes HUISMAN : ``Hypersurfaces réelles et
configurations de pseudo-hyperplans''.
Jeudi 17 octobre 2002:
Yildiray OZAN (Middle East Technical University, Turquie) :
``Algebraic and Hamiltonian Circle Actions''.
Jeudi 24 octobre 2002:
Markus SCHWEIGHOFER (post doc RAAG à Rennes) : ``The real
holomorphy ring of a ring and its iterations''.
Jeudi 31 octobre 2002:
Isabelle BONNARD (Paris 6) : ``Fonctions analytiquement
constructibles''.
Jeudi 7 novembre2002 :
Daniel PANAZZOLO (Sao Paulo) : ``Désingularisation d'un
germe d'un champ de vecteurs de l'espace''.
Jeudi 14 novembre 2002:
Adam PARUSINSKI (Angers) : ``Invariants motiviques des
ensembles
réels''.
Jeudi 21 novembre 2002:
Karim BEKKA : ``Voisinages tubulaires''.
Jeudi 28 novembre 2002:
Karim BEKKA : `` Structure différentiable sur un ensemble
sous-analytique''.
Jeudi 5 décembre 2002:
Ronan QUAREZ : ``Espace des germes d'arcs réels et
série de Poincaré d'un ensemble semi-algébrique''.
Jeudi 12 décembre 2002:
Frédéric MANGOLTE (Chambéry) : ``Morphismes
algébriques vers la sphère standard et surfaces de Del
Pezzo réelles de degré 2''.
Jeudi 16 janvier 2003:
Andreas BERNIG (Zurich) : "Formules de Schlaelfi et courbures
des
ensembles sous-analytiques".
Jeudi 23 janvier 2003:
Erwan BRUGALLE : "Classification des courbes symétriques
de degré 7 dans le plan projectif".
Jeudi 30 janvier2003 :
Didier D'ACUNTO (Madrid, Chambéry) : "Une borne pour la
longueur des trajectoires de gradient de fonctions
définissables".
Jeudi 6 février 2003:
Jean-Yves WELSCHINGER (ENS de Lyon) : "Invariants des
variétés
symplectiques rationnelles réelles de dimension quatre et bornes
inférieures en géométrie énumérative
réelle".
Jeudi 13 février 2003:
Antoine DUCROS : "Sous-ensembles semi-algébriques d'une
variété algébrique p-adique (vue comme espace de
Berkovich)".
Mercredi 19 février2003 :
Sergey FINASHIN (Ankara) : ``The residual
invariants for
the
Seiberg-Witten/Ozsvath-Szabo theories and the adjunction inequality for
membranes''.
Jeudi 20 février 2003:
Michele LATTARULO (Genes) : "Automorphismes imaginaires sur
les
courbes hyperelliptiques réelles".
Vendredi 21 février 2003 :
Gabriel DOS REIS (INRIA Sophia Antipolis) : ``Géometrie et
construction de surfaces à courbure moyenne constante''.
Jeudi 6 mars 2003:
Jean-Philippe MONNIER (Angers) : "Diviseurs sur les courbes
algébriques réelles".
Jeudi 13 mars 2003:
Ilia ITENBERG : "Amibes non archimédiennes et
géométrie énumérative".
Jeudi 20 mars 2003:
Georges COMTE (Nice) : "Localisation des invariants de
Dehn-Weyl".
Jeudi 27 mars 2003:
Goulwen FICHOU (Angers) : "Nombres de Betti virtuels pour les
ensembles symétriques par arcs".
Mercredi 16 avril 2003 :
Vincent FLORENS (Strasbourg) : ``Sur le théorème de
Fox-Milnor pour le polynôme d'Alexander d'un entrelacs''.
Jeudi 17 avril 2003:
Nicolas DUTERTRE (Marseille) : "Sur la caractéristique
d'Euler d'un ensemble algébrique ayant un ensemble singulier
compact".
Jeudi 22 mai 2003:
Johannes HUISMAN : ``Toute 3-variété de Seifert
orientable est une composante réelle d'une variété
uniréglée''.
Jeudi 12
juin 2003:
Eugenii SHUSTIN (Tel Aviv) : ``On real pseudo-holomorphic
non-algebraic curves''.
Jeudi 19 juin 2003:
Alex DEGTYAREV (Ankara) : Towards the quasi-simplicity of real elliptic
surfaces''.
Jeudi 26 juin 2003:
Sergey FINASHIN (Ankara) : ``Invariants of surfaces in
4-manifolds and adjunction inequality for membranes''.
Année
2001-2002

JEUDI 4 octobre 2001 :
Adam PARUSINSKI (Angers) : ``Catégories constructibles et
théorème de Borel-Kurdyka''.
JEUDI 11 octobre 2001 :
Johan HUISMAN: ``Sur la géométrie
énumérative de courbes réelles planes''.
JEUDI 18 octobre 2001 :
Detlev HOFFMANN (Besançon) : ``Relations
d'équivalence pour des formes quadratiques''.
JEUDI 25 octobre 2001 :
Vyacheslav NIKULIN (Liverpool) : ``On automorphism groups of
K3
surfaces''.
JEUDI 8 novembre 2001 :
Rémi SOUFFLET (Dijon) : ``Théorème de
préparation pour les fonctions logarithmico-exponentiel''.
JEUDI 15 novembre 2001 :
séance en commun avec le séminaire de
Géométrie analytique
Laurent BONAVERO (Grenoble) : ``Une caractérisation de la
quadrique complexe''.
JEUDI 22 novembre 2001 :
Jean-Philippe MONNIER (Angers) : ``Diviseurs sur les courbes
réelles''.
JEUDI 29 novembre 2001 :
Lev BIRBRAIR (Valladolid) : ``Metric Homology and
Characteristic
Exponents of Singular Spaces''.
JEUDI 6 décembre 2001 :
Krzysztof KURDYKA (Chambery) : ``Une généralisation
de l'inégalite de gradient pour les applications analytiques''.
MARDI 18 décembre 2001 :
Victor VASSILIEV (Moscou) : ``Combinatorial formulas for
cohomology classes of spaces of knots''.
JEUDI 20 décembre 2001 :
Alexandre GABARD (Genève) : ``Une caractérisation
des courbes réelles séparantes''.
JEUDI 24 janvier 2002 :
Vincent FLORENS (UBS Vannes) : ``Inégalité de
Murasugi-Tristram généralisée et orientations
complexes des M-courbes de degré 7''.
JEUDI 7 février 2002 :
Jean-Yves WELSCHINGER (ENS, Lyon) : ``Structures réelles
sur les surfaces reglées minimales''.
LUNDI 11 février 2002 :
Jesus ESCRIBANO (Madrid) : ``Definable families of definable
stratified sets''.
JEUDI 14 février 2002 :
Jean-Marie TREPREAU (Paris VI) : ``Classification holomorphe
de
courbes planes analytiques''.
JEUDI 28 février 2002 :
Alexander DEGTYAREV (Bilkent) : ``The equivariant moduli
space of
K3-surfaces has finitely many connected components''.
JEUDI 7 mars 2002 :
Michel CROUZEIX : ``Quelques problèmes liés
à l'image numérique d'une matrice carrée''.
JEUDI 14 mars 2002 :
Pierre MILMAN (Toronto) : ``Differentiable functions defined
on
closed sets. A problem of Whitney''.
JEUDI 28 mars 2002 :
Patrick SPEISSEGGER (Université de Madison) : ``Noyau
ouvert et o-minimalité d'une structure sur la ligne
réelle''.
MERCREDI 24 avril 2002 :
János KOLLÁR (Princeton) : `` Which are the
simplest algebraic varieties?''.
JEUDI 25 avril 2002 :
János KOLLÁR (Princeton) : ``The Nash conjecture
for nonprojective threefolds''.
JEUDI 2 mai 2002 :
Jose FERNANDO (Madrid) : "Sums of squares of analytic function germs".
JEUDI 16 mai 2002 :
Jose SEADE (Cuernavaca, Mexique) : "On real singularities with a Milnor
fibration".
JEUDI 23 mai 2002 :
Ján MINÁC (London, Ontario) : "Operation Mountain Tiger
in Galois module theory".
JEUDI 30 mai 2002 :
Markus PFLAUM (Francfort) : "Homology theories of algebras of Whitney
functions over subanalytic sets".
JEUDI 6 juin 2002 :
Vincent GRANDJEAN (Chambéry) : "Infinite relative determinacy of
germs with non isolated singularities and relatiive Lojasiewisz
conditions".
JEUDI 13 juin 2002 :
Abdelhafed ELKHADIRI (Kenitra, Maroc) : "Théorème du
complément pour les ensembles quasi sous analytiques".
JEUDI 20 juin 2002 :
Marie-Françoise ROY : "Descartes, racines virtuelles et
algorithme de Casteljau".
LUNDI 24 juin 2002 :
Abdelhafed ELKHADIRI (Kenitra, Maroc) : "Projections d'ensembles Gevrey
semi-analytiques".
JEUDI 27 juin 2002 :
Benoît BERTRAND: "Courbes et surfaces algébriques
réelles maximales dans des variétés toriques de
dimension 3".
Année
2000-2001

21 septembre 2000:
S. Finashin (Ankara) : Topology of real surface singularities.
5 octobre 2000:
A. Ducros : Courbes de genre 1 sur R(t) et R((t)).
12 octobre 2000 :
J.-M. Lion : Structures o-minimales et croissance
controlée de courbes intégrales.
26 octobre 2000 :
R. Quarez : Espace des germes d'arcs réels tracés
sur un ensemble semi-algébrique.
2 novembre 2000 :
H. Pennaneac'h : Chaines lagrangiennes algébriquement
constructibles.
Mardi 7 novembre 2000 :
O. Viro (Uppsala) : Real algebraic knot theories.
16 novembre 2000 :
F. Morel (Paris 7) : Théorie de l'homotopie, formes
quadratiques et groupes de Chow des cycles orientés.
23 novembre 2000 :
I. Bonnard (Angers) : Fonctions Nash-constructibles.
30 novembre 2000 :
I. Itenberg : Finitude du nombre de structures réelles sur
une surface K3.
7 décembre 2000 :
J.-L. Colliot-Thélène (Orsay) : Formes quadratiques
sur C((x, y)).
14 décembre 2000 :
J. Huisman : Formes quadratiques et classes d'homotopie de
morphismes de la droite projective dans elle-même.
11 janvier 2001 :
A. Aigon (Montpellier) : Equations de courbes et surfaces
hyperboliques en genre 2.
18 janvier 2001 :
K. Bekka : Sur le cône tangent.
Vendredi 19 janvier 2001 :
A. Degtyarev (Bilkent) : Some finiteness results in real
algebraic geometry.
25 janvier 2001:
S. Orevkov (Toulouse) : Classification des M-courbes
pseudo-holomorphes réelles de degré 8.
1 février 2001 :
J.-Y. Welschinger (Strasbourg) : Forme d'intersection tordue
et
extension de la congruence d'Arnol'd.
15 février 2001 :
J.-Ph. Monnier (Angers) : Groupe de Witt des courbes
réelles singulières.
22 février 2001:
G. Comte (Nice) : Equisingularité réelle.
1 mars 2001 :
I. Itenberg : Points critiques de polynômes réels.
Mardi 13 mars 2001 :
à 14 h 00 : A. Parusinski (Angers) :
Méthode de polygone de Newton relatif à une courbe.
à 16 h 00 : S. Koike (Hyogo) :
Equisingularity
problem of real algebraic singularities.
22 mars 2001 :
J. Huisman : Sur le nombre d'ovales d'une courbe gauche
réelle.
29 mars 2001 :
J.-J. Risler (Paris VI) : Sur la courbure de la fibre de
Milnor.
19 avril 2001:
N. Dutertre (Barcelone) : Courbure et singularités
réelles.
26 avril 2001:
J. Huisman : Sur le dual d'une hypersurface analytique
réelle.
3 mai 2001:
P. Balmer (Münster) : Groupes de Witt et catégories
triangulées.
10 mai 2001 :
D. Derval : Sur les cycles algébriques d'une
variété algébrique réelle obtenue à
partir d'une modification.
17 mai 2001 :
J. Königsmann (Konstanz) : Encoding valuations in absolute Galois
groups.
Mardi 22 mai 2001 :
J. Königsmann (Konstanz) : Model theoretic versus field
theoretic algebraic closure.
31 mai 2001 :
K. Becher (Besançon) : Corps non réels avec un
nombre de classes de carrés fini.
Lundi 18 juin 2001 :
G. Mikhalkin (University of Utah) : Topology of algebraic
hypersurfaces.
Mardi 19 juin 2001 :
O. Viro (Uppsala University) : Khovanov homology of classical
links.
Mercredi 20 juin 2001 :
à 10 h 30 : S. Finashin (Middle East Technical University)
: Seiberg-Witten invariants for surfaces in 4-manifolds.
à 13 h 30 : A. Gabrielov (Purdue) :
Degrees of
Real Grassmann Varieties.
21 juin 2001 :
A. Degtyarev (Bilkent Univeristy) : Klein actions on complex
tori.
Année
1999-2000

7 octobre 1999 :
J. Huisman : Sur le groupe fondamental d'une courbe algébrique
réelle.
14 octobre 1999 :
M. Tibar (Lille) : Feuilles séparatrices d'un feuilletage
algébrique.
21 octobre 1999 :
J. Escribano (Madrid / Rennes) : Nash triviality in
families of Nash mappings
28 octobre 1999 :
A. Diaz-Cano (Madrid / Rennes) : Complexity of global semianalytic
sets.
4 novembre 1999 :
M. Coste : Propriétés globales des fonctions de Nash
: tranfert et bornes uniformes.
18 novembre 1999 :
T. Sturm (Passau) : Providing real solutions.
F. Rouillier (Nancy) : RS: solutions réelles.
25 novembre 1999:
S. Koike (Hyogo) : Computations and stability of the Fukui invariant.
2 décembre 1999:
N. Dutertre : Sur la caractéristique d'Euler d'intersections
complètes à singularités isolées.
9 décembre 1999:
I. Itenberg : Topologie des hypersurfaces réelles combinatoires.
16 décembre 1999:
V. Grandjean : Discriminant résiduel de quelques
singularités non isolées.
13 janvier 2000:
M. Coste : Valeurs atypiques à l'infini de polynomes
réels en deux variables.
20 janvier 2000:
J. Escribano (Madrid / Rennes) : An approximation
theorem
for definable mappings.
27 janvier 2000:
S. Orevkov (Toulouse) : Topologie des courbes algébriques
réelles et courbes pseudo-holomorphes réelles.
10 février 2000:
J. Huisman : Courbes gauches algébriques ayant beaucoup de
branches réelles et peu de points d'inflexion.
2 mars 2000:
A. Bernig (Münster) : Espaces d'Alexandrov dans les
structures o-minimales.
9 mars 2000 :
K. Bekka : Sur l'homologie des espaces stratifiés.
30 mars 2000:
A. Fekak (Casablanca) : Géométrie semi-algébrique
p-adique, analogie avec le cas réel.
31 mars 2000 :
D. Hoffman (Besancon) : Le nombre de Pythagore d'un
corps.
D. Leep (Univ. de Kentucky) : Pencils of quadratic
forms
and hyperelliptic function fields.
6 avril 2000:
P. Orro (Chambery) : Valeurs critiques
généralisées et théorème de Sard.
13 avril 2000:
J. Huisman : Sur la composante neutre de l'ensemble des points
réels de la Jacobienne d'une courbe.
4 mai 2000:
F. Bihan (Genève) : Sur les valeurs asymptotiques des
nombres de Betti d'hypersurfaces algébriques d'espaces
projectifs réels.
11 mai 2000:
J-Ph. Monnier (Angers) : Groupe de Witt et torsion dans le
groupe
de Picard pour les courbes
algébriques réelles.
18 mai 2000:
A. Rosly (Moscou) : Polar homology
15 juin 2000 :
A. Degtyarev (Univ. de Bilkent) : Real quantum cohomology --
perspectives and applications.
22 juin 2000 :
pas de séance
29 juin 2000 :
L. Mahé : Généralisation d'ordres et
clôtures associées.
|

 Retour à la page
actuelle du séminaire
Retour à la page
actuelle du séminaire 
 Retour à la page
actuelle du séminaire
Retour à la page
actuelle du séminaire 
