Université de Rennes 1

mardi 5 octobre

Mathilde Herblot

Courbes elliptiques

Résumé : on s'intéressera aux points de torsion d'une courbe elliptique.

mardi 12 octobre

Sandrine Caruso

Présentation du groupe de tresses étendu

Résumé :

Le groupe de tresses à n brins, que l’on peut définir comme B_n = π₁(S ⊂ R², Card(S) = n), a une présentation par générateurs et relations classique :

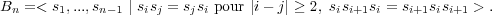
Dans cet exposé, on s’intéresse au groupe de tresses à n brins autour d’une tige fixe (ou groupe de tresses étendu à n brins), défini comme 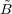_n = π₁(S ⊂ C^*, Card(S) = n), dont on veut établir la présentation similaire suivante :

mercredi 20 octobre

Damian Brotbek

Une petite introduction à l'hyperbolicité

Résumé : Dans cet exposé, je vais essayer d'expliquer un peu ce qu'est l'hyperbolicité en géométrie complexe. Je parlerai aussi d'espace de jets, de calcul d'intersection, et de positivité de diviseur, le but principal étant d'introduire les notions dont je vais avoir besoin dans la séance suivante.

mardi 2 novembre

Damian Brotbek

Une petite introduction à l'hyperbolicité (suite)

mercredi 3 novembre

Sabine Burgdorf (Université de Constance)

Le problème des moments traciaux

Résumé : Le problème des moments traciaux demande à la caractérisation des formes linéaires traciales, qui sont données par des moments traciaux d'une mesure de probabilité sur des matrices symétriques de taille fixée. Il est le problème dual du problème de la caractérisation des polynômes à trace positive. Certains résultats concernant le problème classique des moments peuvent être reformulés dans le contexte tracial. Concrètement, après une introduction qui revoit le problème classique des moments je présente le problème des moments traciaux ainsi que des versions traciales de théorèmes de Stochel, de Haviland, et de Curto et Fialkow.

mardi 9 novembre

Julien Dhondt

Recollement de fonctions analytiques sur un corps local.

Résumé : On considère un corps K ultramétrique\A0complet. K^r est muni de la norme infinie et on note D son disque unité. Une fonction analytique (au sens fort) sur D sera, ici, une application de D dans K, globalement somme d'une série entière. Or D peut être recouvert par des boules ouvertes disjointes de rayon strictement inférieur à 1 (propriété topologique des espaces vectoriels normés ultramétriques). Un tel recouvrement ne permet pas de\A0\AB\A0recoller \BBles fonctions analytiques. Cette notion d'analycité n'est donc pas de nature locale. On peut cependant mettre en évidence certaines classes de recouvrements ouverts du disque unité possédant une propriété de recollement, c'est à dire permettant de recoller les fonctions comme en géométrie complexe, ainsi que le montre Tate.

mercredi 17 novembre

Clément Dunand

Maths et musique.

Résumé : beaucoup moins profond et théorique que les précédents, cet exposé est tiré d'un petit complément proposé dans un cours de L2 biologie. Je vous raconterai les fondements arithmétiques de la gamme ainsi que le principe des harmoniques dans un signal sonore...tout en veillant à ce qu'il n'y ait aucun prérequis musical à la bonne compréhension de l'exposé.

mercredi 24 novembre

Anna Morra

Comptage asymptotique d'extensions cubiques avec résolvante quadratique fixée

Résumé : Soit k un corps de nombres et K_2 une extension quadratique de k. Je vais montrer comment on trouve une formule asymptotique pour le nombre de classes d'isomorphisme des extensions cubiques K de k telles que la clôture de Galois de K/k contient K_2 comme sous-extension quadratique. L'outil principal est la théorie de Kummer. On pourra retrouver aussi le cas des extensions cycliques cubiques (correspondant à K_2 = k) comme cas particulier.

mardi 30 novembre

Jérémy Le Borgne

Un peu d'analyse p-adique

Résumé : J'expliquerai les bases de l'analyse p-adique, en expliquant la construction des corps p-adiques ainsi que les propriétés topologiques associées, et quelques résultats sur la structure des espaces fonctionnels.

mardi 7 décembre

Relâche

mardi 14 décembre

Xavier Caruso

Fractions continues et construction de gammes musicales

Résumé : Cet exposé fait suite à l'exposé de Clément intitulé "Maths et musique". On y voit comment un développement en fractions continues permet de retrouver et de comprendre différemment les nombres de notes intervenant dans les gammes utilisées par les musiciens.
Un petit texte de Xavier reprenant et précisant le contenu de son exposé.

jeudi 13 janvier

Fabien Priziac

Filtration par le poids pour les variétés algébriques réelles

Résumé : En 1972, Pierre Deligne associe à toute variété algébrique complexe une filtration dite par le poids sur la cohomologie rationnelle de la variété. En 2008, Clint McCrory et Adam Parusinski ont montré le pendant réel de ce résultat en prouvant l'existence d'une filtration par le poids pour toute variété algébrique réelle. Cet exposé reprendra pour la plus grande part la première partie de leur article consacré à ce dernier résultat et, si le temps le permet, je parlerai de mon travail en cours, à savoir la recherche d'une filtration par le poids "équivariante" pour toute variété algébrique réelle munie d'une action d'un groupe fini par isomorphismes algébriques.

jeudi 20 janvier

Sandrine Caruso

Pavages hyperboliques et surfaces fermées de genre > 1

Résumé : Dans cet exposé, on décrira les pavages réguliers du plan hyperbolique, puis on verra comment utiliser de tels pavages pour munir des surfaces de genre supérieur ou égal à 2 d'une métrique hyperbolique.

jeudi 27 janvier

Matthieu Legeay

Codes correcteurs d'erreurs

Résumé : Bienvenue dans le monde merveilleux des codes correcteurs d'erreurs : après un bref mais suffisant rappel sur les généralités des codes correcteurs, je vous présenterai différentes classes de tels codes avec les particularités/avantages/inconvénients de chacun. Un voyage au pays des corps finis !

jeudi 3 février

Relâche (Journées Louis Antoine)

mercredi 23 février, salle 16, 14h

Matthieu Calvez

Des tresses en bon ordre

Résumé : P. Dehornoy a montré dans les années 90 que le groupe des tresses Bn est ordonnable à gauche. On discutera quelques propriétés de cet ordre, notamment le caractère bien ordonné du monoïde des tresses positives Bn+.

jeudi 3 mars, 14h30

Christophe Wacheux

La méthode du chemin de Moser en géométrie symplectique et ses applications

Résumé : En géométrie symplectique, comme dans d'autres domaine de géométrie différentielle on est souvent intéressé de savoir si deux variétés, accompagnées de structures supplémentaires, sont équivalentes, c'est à dire s'il existe un difféomorphisme préservant ces structures. Dans le cas de la géométrie symplectique, la méthode du chemin de Moser consiste à chercher ce difféomorphisme comme le flot au temps 1 d'un certain champ de vecteurs, qu'il s'agit ensuite de déterminer. Dans l'exposé, après un bref rappel de géométrie symplectique nous présenterons d'abord le principe de cette méthode de déformation isotopique. Dans un deuxième temps, nous montrerons comment cette méthode intervient dans la démonstration de beaucoup de résultats de géométrie symplectique. Si j'ai le temps, je tenterai de vous montrer l'utilisation que j'en ai faite dans un papier en cours de soumission.